1. Moment của hình ảnh

Moment hình ảnh (Image moment) nghe có vẻ rất trìu tượng? Thực ra nó đơn giản là một công cụ giúp chúng ta tính toán một số đặc điểm như khối tâm của vật thể, diện tích của vật thể, ... Hàm cv2.moments() cung cấp một tập hợp của tất cả các giá trị moment có thể tính toán. Xem đoạn code minh họa bên dưới:

1. import cv2
2. import numpy as np
4. img = cv2.imread('sign.jpg', 0)
5. imgray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
6. ret, thresh = cv2.threshold(imgray, 127, 255, 0)
7. contours, hierarchy = cv2.findContours(thresh, 1, 2)
9. cnt = contours[0]
10. M = cv2.moments(cnt)
11. print(M)

Từ những giá trị moment này, chúng ta có thể trích xuất dữ liệu hữu ích như khu vực, trung tâm,... Trọng tâm có thể được tính toán thông qua công thức: C_x = M₁₀ / M₀₀ và C_y = M₀₁ / M₀₀. Điều này có thể được thực hiện như sau:

12. cx = int(M['m10'] / M['m00'])
13. cy = int(M['m01'] / M['m00'])

2. Khu vực đường viền

Vùng đường viền thu được bởi hàm cv2.contourArea() hoặc từ các moment M ['m00']:

14. area = cv2.contourArea(cnt)

3. Chu vi đường viền

Còn được gọi là độ dài cung, chu vi đường viền có thể được tìm ra bằng cách sử dụng hàm cv2.arcLength(), truyền vào 2 đối số, trong đó, đối số thứ hai chỉ định hình dạng là một đường viền khép kín (nếu được truyền “True”) hoặc chỉ là một đường cong:

15. perimeter = cv2.arcLength(cnt, True)

4. Đường viền xấp xỉ

Tức là lấy xấp xỉ một đường viền thành một hình dạng khác với số lượng đỉnh ít hơn tùy thuộc vào độ chính xác mà chúng ta chỉ định, sử dụng thuật toán Douglas-Peucker.

Giả sử chúng ta đang cố gắng tìm một hình vuông trong một hình ảnh, nhưng do một số vấn đề trong hình ảnh, không thể có được một hình vuông hoàn hảo mà là một “hình dạng xấu xí”. Lúc này bạn có thể sử dụng hàm cv2.approxPolyDP() để ước lượng hình dạng. Trong đó, đối số thứ hai được gọi là epsilon, là khoảng cách tối đa từ đường viền đến đường gần đúng. Nó là một tham số chính xác. Cần có sự lựa chọn khéo léo đối với epsilon để có được đầu ra chính xác. Đối số thứ ba chỉ định xem đường cong có được đóng hay không:

16. epsilon = 0.1*cv2.arcLength(cnt, True)
17. approx = cv2.approxPolyDP(cnt, epsilon, True)

5. Đường lồi

Hàm cv2.convexHull() kiểm tra một đường cong để tìm các khuyết tật lồi và sửa nó. Nói chung, đường cong lồi là những đường cong luôn luôn bị phình ra, hoặc ít nhất là bằng phẳng. Và nếu nó bị phình ra bên trong, nó được gọi là khuyết tật lồi lõm. Ví dụ, hãy kiểm tra hình ảnh dưới đây của bàn tay. Đường màu đỏ cho thấy phần lồi của bàn tay. Các dấu mũi tên hai mặt cho thấy các khuyết tật lồi lõm, là sai lệch tối đa cục bộ của thân so với các đường viền.

Cú pháp:

18. hull = cv2.convexHull(points[, hull[, clockwise[, returnPoints]]

Chi tiết các đối số:

- points là các đường viền mà chúng ta truyền vào.

- hull là đầu ra.

- clockwise là cờ định hướng. Nếu nó là True, convex hull đầu ra được định hướng theo chiều kim đồng hồ. Nếu không, nó được định hướng ngược chiều kim đồng hồ.

- returnPoints theo mặc định là True và trả về tọa độ của các điểm đầu ra. Nếu False, nó trả về chỉ số của các điểm đường viền tương ứng với các điểm đầu ra. Nếu muốn tìm khuyết tật lồi, chúng ta cần phải truyền returnPoints = False.

Hàm thực thi trong thực tế có dạng đơn giản như sau:

19. hull = cv2.convexHull(cnt)

6. Kiểm tra độ lồi

Có một hàm để kiểm tra xem một đường cong có lồi hay không, đó là cv2.isContourConvex(). Nó chỉ trả về True hoặc False:

20. k = cv2.isContourConvex(cnt)

7. Hình chữ nhật bao quanh

Có hai loại hình chữ nhật bao quanh:

7.a. Hình chữ nhật có đường viền ngay ngắn

Là một hình chữ nhật ngay ngắn, không xem xét chuyển động quay của vật thể và được tính toán bởi hàm cv2.boundsRect(), do đó, diện tích của hình chữ nhật giới hạn sẽ không phải là nhỏ nhất. Gọi (x, y) là tọa độ trên cùng bên trái của hình chữ nhật và (w, h) là chiều rộng và chiều cao của nó:

10. x,y,w,h = cv2.boundingRect(cnt)
11. cv2.rectangle(img, (x,y), (x+w,y+h), (0,255,0), 5)

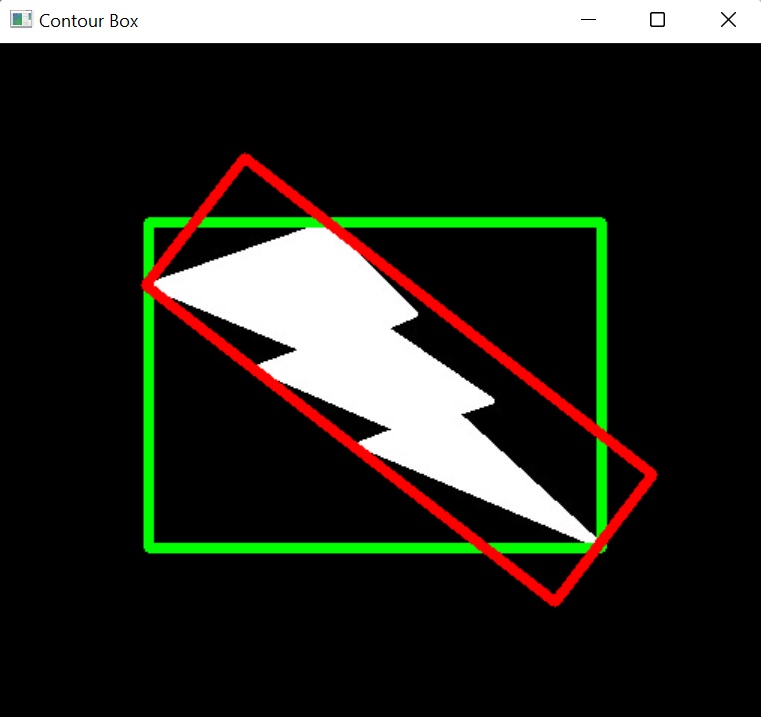
7.b. Hình chữ nhật đã xoay

Ở đây, hình chữ nhật giới hạn được vẽ với diện tích tối thiểu, vì vậy nó có thể bị xoay. Hàm được sử dụng là cv2.minAreaRect(), trả về một cấu trúc hộp 2D chứa các thông tin sau: tâm(x, y), (chiều rộng, chiều cao), góc quay. Để vẽ được hình chữ nhật này, chúng ta cần 4 góc của hình chữ nhật bởi hàm cv2.boxPoints():

12. rect = cv2.minAreaRect(cnt)
13. box = cv2.boxPoints(rect)
14. box = np.int0(box)
15. cv2.drawContours(img, [box], 0, (0,0,255), 5)
17. cv2.imshow(‘Contours Box’, img)
18. cv2.waitKey(0)
19. cv2.destroyAllWindows()

Kết quả:

8. Vòng tròn bao quanh tối thiểu

Tiếp theo, chúng ta tìm đường tròn ngoại tiếp của một đối tượng bằng cách sử dụng hàm cv2.minEnclosingCircle(). Nó là một hình tròn bao phủ hoàn toàn vật thể với diện tích tối thiểu:

10. (x, y), radius = cv2.minEnclosingCircle(cnt)
11. center = (int(x), int(y))
12. radius = int(radius)
13. cv2.circle(img, center, radius, (255,0,0), 5)

9. Hình elip bao quanh

Tiếp theo là lắp một hình elip vào một đối tượng. Nó trả về hình chữ nhật xoay trong đó hình elip được nội tiếp:

14. ellipse = cv2.fitEllipse(cnt)
15. cv2.ellipse(img, ellipse, (0,255,0), 5)

10. Đường nối

Tương tự, chúng ta có thể nối một đoạn thẳng với một tập hợp các điểm. Hình ảnh dưới đây chứa một tập hợp các điểm màu trắng. Chúng ta có thể tính gần đúng một đường thẳng với chúng:

16. rows, cols = img.shape[:2]
17. [vx, vy, x, y] = cv2.fitLine(cnt, cv2.DIST_L2, 0, 0.01, 0.01)
18. lefty = int((-x*vy/vx) + y)
19. righty = int(((cols-x)*vy/vx) + y)
20. cv2.line(img, (cols-1, righty), (0, lefty), (0,0,255), 5)
22. cv2.imshow(‘Contours Box’, img)
23. cv2.waitKey(0)
24. cv2.destroyAllWindows()

 Kết quả:

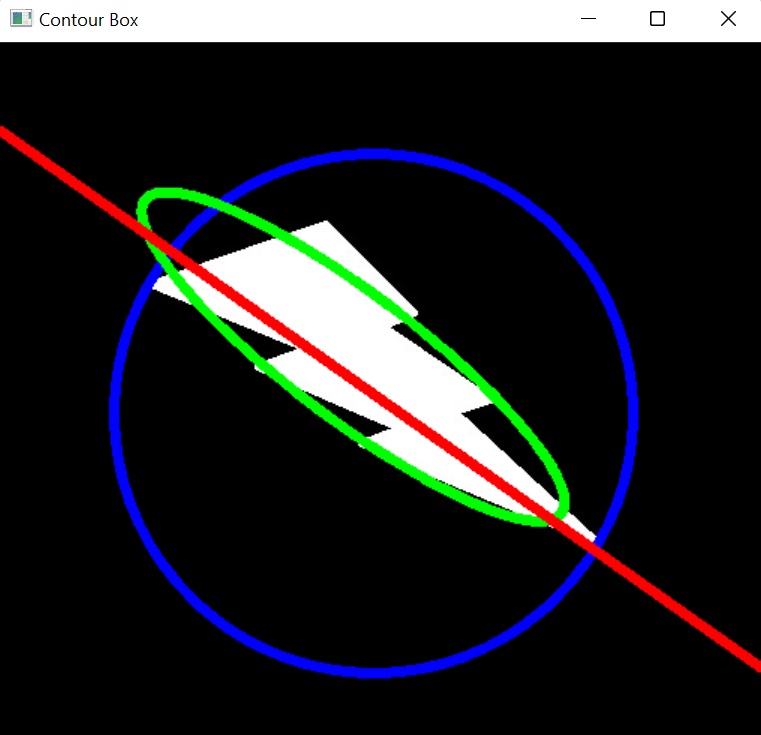
Ở phần tiếp theo chúng ta sẽ cùng tìm hiểu về biểu đồ hình ảnh.

(Sưu tầm)
VIỆN IMC
Tòa nhà IMC Tower, Số 176 Trường Chinh, Phường Khương
Thượng, Quận Đống Đa, Thành phố Hà Nội, Việt Nam
Tel/Fax : (+84) 24 3566 6232 / 24 3566 6234
Email: contact@imc.org.vn   Website: https://imc.org.vn